Talvez não tenha aula na próxima segunda, talvez tenha. Tudo dependerá da Jornada Acadêmica (aqueles trabalhos que serão apresentados dias 19-21). Se tiver jornada, nada de aula.
Na outra segunda (26/05) também não deve ter aula, pois ela estará aplicando a prova para a outra turma. Então essa provavelmente será a última aula antes da prova.
Diz Aquele que Rege que a prova será nos moldes desses exercícios. Caberá a cada um de vocês ter fé.
Exercício
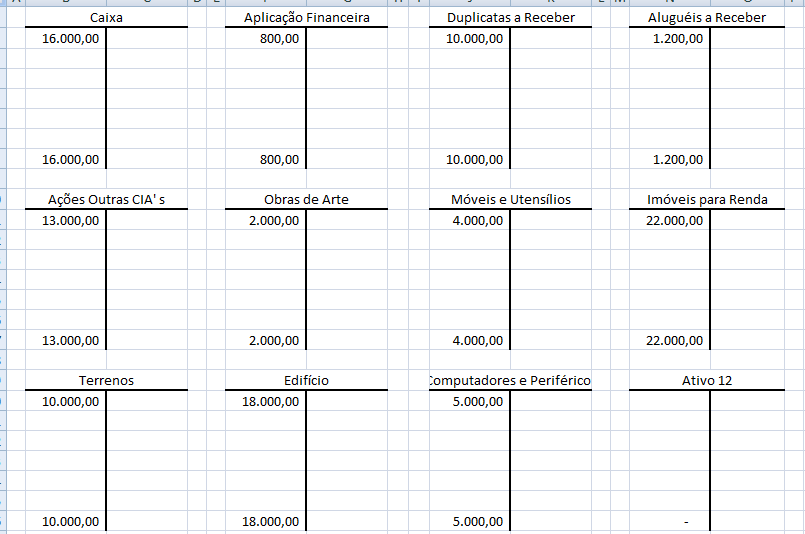
Lance os dados no Razão;
Elabore dois balancetes, sendo um com as contas de resultado e outro apenas com contas patrimoniais;
Faça o Balanço.
Ativo
1º Balancete de Verificação
 Atenção, deve seguir a ordem: Ativo Circulante, A-nC Realizável LP, , A-nC Investimentos, A-nC Imóveis, A-nC Intangível, Passivo Circulante, P-nC, PL, Receitas e depois Despesas.
Atenção, deve seguir a ordem: Ativo Circulante, A-nC Realizável LP, , A-nC Investimentos, A-nC Imóveis, A-nC Intangível, Passivo Circulante, P-nC, PL, Receitas e depois Despesas.

 A conta "Resultado do Exercício" ficou com um saldo Credor, certo?
A conta "Resultado do Exercício" ficou com um saldo Credor, certo?
Isso significa que o resultado foi positivo, ou seja, Lucro. Então abrimos a conta "Lucro Acumulado" para então passarmos esse saldo para lá. E como fazemos isso? Debitando "Resultado" e creditando "Lucro Acumulado".
 2º Balancete de Verificação
2º Balancete de Verificação
 Note que o segundo balancete deve bater em valor com o Balanço Patrimonial.
Note que o segundo balancete deve bater em valor com o Balanço Patrimonial.




 Na sala ela falou que precisaria fazer os dois balancetes. Ao final da aula ela voltou atrás e disse que bastava o com as contas patrimoniais. Por isso estou colocando os dois aqui.
Na sala ela falou que precisaria fazer os dois balancetes. Ao final da aula ela voltou atrás e disse que bastava o com as contas patrimoniais. Por isso estou colocando os dois aqui.
Na outra segunda (26/05) também não deve ter aula, pois ela estará aplicando a prova para a outra turma. Então essa provavelmente será a última aula antes da prova.
Diz Aquele que Rege que a prova será nos moldes desses exercícios. Caberá a cada um de vocês ter fé.
Exercício
Lance os dados no Razão;
Elabore dois balancetes, sendo um com as contas de resultado e outro apenas com contas patrimoniais;
Faça o Balanço.
Duplicatas a
Receber
|
10.000
|
Duplicatas a Pagar
|
2.000
|
Duplicatas a Pagar
24 meses
|
1.000
|
Aluguéis Recebidos
|
1.000
|
Aluguéis Pagos
|
500
|
Aluguéis a Receber
|
1.200
|
Aluguéis a Pagar
|
800
|
Caixa
|
16.000
|
Aplicação
Financeira
|
800
|
Combustíveis
|
450
|
Telefonemas
|
200
|
Internet
|
200
|
Ações de outras
CIAs
|
13.000
|
Obras de Arte
|
2.000
|
Móveis e
Utensílios
|
4.000
|
Despesas de
Material de Limpeza
|
250
|
Venda de Serviços
|
8.000
|
Venda de
Mercadorias
|
10.000
|
Propaganda e
Publicidade
|
1.200
|
Imóveis para Renda
|
22.000
|
Terrenos
|
10.000
|
Edifício
|
18.000
|
Viagens e Estadas
|
600
|
Computadores e
Periféricos
|
5.000
|
Financiamento de
Longo Prazo
|
26.600
|
Capital Social
|
56.000
|
Ativo
Passivo
Patrimônio Líquido
Despesas e Receitas
Despesas e Receitas não aparecem no Balanço Patrimonial, então devemos integra-las ao PL. Fazemos isso por alguns lançamentos a mais:
Abrimos a conta "Resultado do Exercício" e lançamos os valores das despesas e das receitas nela.
Como fazemos isso? Debitando e Creditando as devidas contas. Ou seja, agora vamos zera-las.
Isso significa que o resultado foi positivo, ou seja, Lucro. Então abrimos a conta "Lucro Acumulado" para então passarmos esse saldo para lá. E como fazemos isso? Debitando "Resultado" e creditando "Lucro Acumulado".
Aula do dia 13/05
Outro exercício bem semelhante ao anterior.


Ei a ordem do ativo não circulante n~ é imobilizado, investimento, intangível ?
ResponderExcluirNão, é Investimento, Imobilizado e Intangível mesmo.
ResponderExcluir